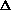jobs with weight w, and n
jobs with weight w,
all having processing time
p, and given a batch setup time 
, find a sequence of batches of
jobs such that the weighted sum of the n = n + n
job completion times is minimized.
The algorithm has running time O(n
logn) when p and
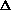are fixed; previously,
the fastest known algorithm for this problem had running time O(n).
Various properties of optimal solutions are exploited to reduce the problem
to one of finding the minimum entry in a certain matrix. Since this
matrix has some strong structural properties, its minimum entry can
be found in time that is a sublinear function of the matrix size.
Click on the following title to view and download the paper in PostScript format.
- Scheduling with Batching: Two Job Types (14 pages, 145 KB)
- Dorit S. Hochbaum and D. Landy. Discrete Applied Math, 72, 99-114, (1997).