
Generalized p-Center Problems: Complexity Results and Approximation Algorithms
Abstract
In an earlier paper [Hud91], two "alternative" p-Center problems,
where the centers serving customers must be chosen so that exactly
one node from each of p prespecified disjoint pairs of nodes
is selected, were shown to be NP-complete.
This paper considers a generalized version of these problems, in which the
nodes from which the p servers are to be selected are partitioned into
k sets and the number of servers selected from each set must be within
a prespecified range. We refer to these problems as the "Set" p-Center problems.
We establish that the triangle inequality (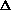 -inequality) versions
of these problems, in which the edge weights are assumed to satisfy
the triangle inequality, are also NP-complete.
We also provide a polynomial time approximation algorithm for the two
-inequality) versions
of these problems, in which the edge weights are assumed to satisfy
the triangle inequality, are also NP-complete.
We also provide a polynomial time approximation algorithm for the two
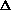 -inequality "Set" p-Center problems that is optimal for one of the
problems in the sense that no algorithm with polynomial running time
can provide a better constant factor performance guarantee, unless P=NP.
-inequality "Set" p-Center problems that is optimal for one of the
problems in the sense that no algorithm with polynomial running time
can provide a better constant factor performance guarantee, unless P=NP.
For the special case "alternative" p-Center problems, which we refer to as the
"Pair" p-Center problems, we extend the results in [Hud91] in several ways.
For example, the results mentioned above for the "Set" p-Center problems also
apply to the "Pair" p-Center problems. Furthermore, we establish and
exploit a correspondence between satisfiability and the dominating
set type of problems that naturally arise when considering
the decision versions of the "Pair" p-Center problems.
Download Information
Click on the following title to view and download the paper in PostScript format.
- Generalized p-Center Problems: Complexity Results and Approximation Algorithms (19 pages, 193 KB)
,
- Dorit S. Hochbaum and Anu Pathria. European Journal of Operational Research, 100:3 1997, 594-607.
dorit@hochbaum.ieor.berkeley.edu
7/30/98

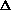 -inequality) versions
of these problems, in which the edge weights are assumed to satisfy
the triangle inequality, are also NP-complete.
We also provide a polynomial time approximation algorithm for the two
-inequality) versions
of these problems, in which the edge weights are assumed to satisfy
the triangle inequality, are also NP-complete.
We also provide a polynomial time approximation algorithm for the two
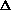 -inequality "Set" p-Center problems that is optimal for one of the
problems in the sense that no algorithm with polynomial running time
can provide a better constant factor performance guarantee, unless P=NP.
-inequality "Set" p-Center problems that is optimal for one of the
problems in the sense that no algorithm with polynomial running time
can provide a better constant factor performance guarantee, unless P=NP.