
Locating centers in dynamically changing network and related problems
Abstract
In a dynamically changing network the costs or distances between
locations are changing in each discrete time period. We consider
the location of emergency facilities that must minimize the
maximum distance to any customer on the network across all
time periods. We call the problem of locating p centers over k
underlying networks corresponding to k periods the
k-Network p-Center problem. The problem is considered when in each period the
network satisfies the
triangle inequality.
In this paper we provide a polynomial time 3-approximation algorithm for
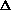 k-Network p-Center for the case k = 2.
k-Network p-Center for the case k = 2.
We discuss generalizations inspired by this problem to other
optimization problems with
multiple underlying networks and the objective of finding a single
solution that varies as little as possible from the optimum for
each network.
The additional combinatorial problems discussed include: sorting;
perfect matching; shortest path; minimum spanning tree; and minimum
cut. All are shown to be NP-hard for k  2.
2.
Download Information
Click on the following title to view and download the paper in PostScript format.
- Locating centers in dynamically changing network and related problems (14 pages, 202 KB)
,
- Dorit S. Hochbaum and Anu Pathria. Manuscript (December 1996). To appear in Location Science.
dorit@hochbaum.ieor.berkeley.edu
7/30/98

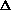 k-Network p-Center for the case k = 2.
k-Network p-Center for the case k = 2.  2.
2.